11.11.2015 Взять и поделить или деление по модулю
Материал из SRNS
Korogodin (обсуждение | вклад) (→Классический %) |
Korogodin (обсуждение | вклад) (→Классический %) |
||
| Строка 58: | Строка 58: | ||
* '''uint a % int b = b<0 ? a : mod(a, b)''' - взятие uint % отрицательного числа - холостая операция, результат - исходный uint | * '''uint a % int b = b<0 ? a : mod(a, b)''' - взятие uint % отрицательного числа - холостая операция, результат - исходный uint | ||
* '''int a % int b = sign(a) * mod(|a|, |b|)''' - знак базы игнорируется, что противоречит интуитивному пониманию и mod в MATLAB | * '''int a % int b = sign(a) * mod(|a|, |b|)''' - знак базы игнорируется, что противоречит интуитивному пониманию и mod в MATLAB | ||
| + | * int a % int b ведет себя как функция mod в MATLAB только при совпадении знаков аргументов, иначе есть смещение на b (за исключением точек, в которых результат ноль). | ||
Для наглядности построены графики (доступен fig): | Для наглядности построены графики (доступен fig): | ||
[[file:20151111_OperatorPerc.png|center]] | [[file:20151111_OperatorPerc.png|center]] | ||
| + | [[file:20151111_OperatorPerc2.png|center]] | ||
== fmod == | == fmod == | ||
Версия 11:55, 12 ноября 2015
|
Есть некоторая неуверенность в результатах работы функций взятия по модулю, для борьбы с которой составлена эта памятка.
Ниже представлены результаты, полученные на Oryx 161, компилятор из Xilinx SDK 2014.4 ( gcc version 4.8.3 20140320 (prerelease) (Sourcery CodeBench Lite 2014.05-23)).
Классический %
Оператор %
(int(13)) % (int(-17)) = 13
(int(13)) % (int(-7)) = 6
(int(13)) % (int(-5)) = 3
(int(13)) % (int(-1)) = 0
(int(13)) % (int(1)) = 0
(int(13)) % (int(5)) = 3
(int(13)) % (int(7)) = 6
(int(13)) % (int(17)) = 13
(int(-13)) % (int(-17)) = -13
(int(-13)) % (int(-7)) = -6
(int(-13)) % (int(-5)) = -3
(int(-13)) % (int(-1)) = 0
(int(-13)) % (int(1)) = 0
(int(-13)) % (int(5)) = -3
(int(-13)) % (int(7)) = -6
(int(-13)) % (int(17)) = -13
(unsigned int(13)) % (int(-17)) = 13
(unsigned int(13)) % (int(-7)) = 13
(unsigned int(13)) % (int(-5)) = 13
(unsigned int(13)) % (int(-1)) = 13
(unsigned int(13)) % (int(1)) = 0
(unsigned int(13)) % (int(5)) = 3
(unsigned int(13)) % (int(7)) = 6
(unsigned int(13)) % (int(17)) = 13
(int(13)) % (unsigned int(1)) = 0
(int(13)) % (unsigned int(5)) = 3
(int(13)) % (unsigned int(7)) = 6
(int(13)) % (unsigned int(17)) = 13
(int(-13)) % (unsigned int(1)) = 0
(int(-13)) % (unsigned int(5)) = 3
(int(-13)) % (unsigned int(7)) = 5
(int(-13)) % (unsigned int(17)) = 5
(unsigned int(13)) % (unsigned int(1)) = 0
(unsigned int(13)) % (unsigned int(5)) = 3
(unsigned int(13)) % (unsigned int(7)) = 6
(unsigned int(13)) % (unsigned int(17)) = 13
(int(13)) % (int(-7)) = 6
(int(13)) % (int(-5)) = 3
(int(13)) % (int(-1)) = 0
(int(13)) % (int(1)) = 0
(int(13)) % (int(5)) = 3
(int(13)) % (int(7)) = 6
(int(13)) % (int(17)) = 13
(int(-13)) % (int(-17)) = -13
(int(-13)) % (int(-7)) = -6
(int(-13)) % (int(-5)) = -3
(int(-13)) % (int(-1)) = 0
(int(-13)) % (int(1)) = 0
(int(-13)) % (int(5)) = -3
(int(-13)) % (int(7)) = -6
(int(-13)) % (int(17)) = -13
(unsigned int(13)) % (int(-17)) = 13
(unsigned int(13)) % (int(-7)) = 13
(unsigned int(13)) % (int(-5)) = 13
(unsigned int(13)) % (int(-1)) = 13
(unsigned int(13)) % (int(1)) = 0
(unsigned int(13)) % (int(5)) = 3
(unsigned int(13)) % (int(7)) = 6
(unsigned int(13)) % (int(17)) = 13
(int(13)) % (unsigned int(1)) = 0
(int(13)) % (unsigned int(5)) = 3
(int(13)) % (unsigned int(7)) = 6
(int(13)) % (unsigned int(17)) = 13
(int(-13)) % (unsigned int(1)) = 0
(int(-13)) % (unsigned int(5)) = 3
(int(-13)) % (unsigned int(7)) = 5
(int(-13)) % (unsigned int(17)) = 5
(unsigned int(13)) % (unsigned int(1)) = 0
(unsigned int(13)) % (unsigned int(5)) = 3
(unsigned int(13)) % (unsigned int(7)) = 6
(unsigned int(13)) % (unsigned int(17)) = 13
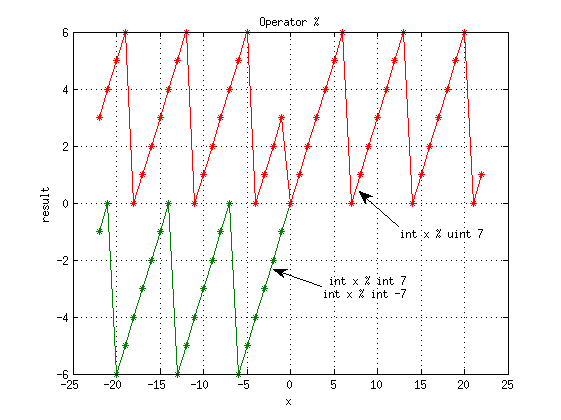
Следует обратить внимание:
- int a % uint b = mod(*(uint*(&a)), b) - результаты для -13%(int 7) и -13%(uint 7) различаются; если брать int % uint, то int интерпретируется как uint, например, -1 превращается в 2^32-1.
- uint a % int b = b<0 ? a : mod(a, b) - взятие uint % отрицательного числа - холостая операция, результат - исходный uint
- int a % int b = sign(a) * mod(|a|, |b|) - знак базы игнорируется, что противоречит интуитивному пониманию и mod в MATLAB
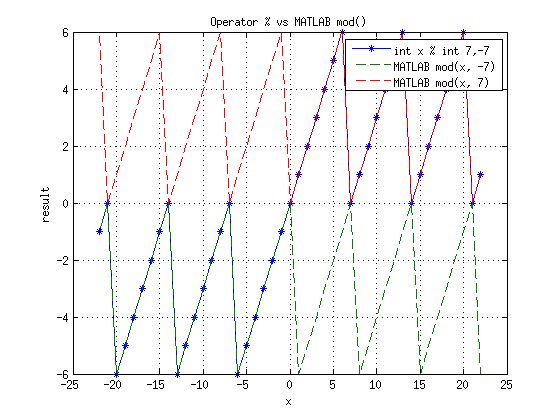
- int a % int b ведет себя как функция mod в MATLAB только при совпадении знаков аргументов, иначе есть смещение на b (за исключением точек, в которых результат ноль).
Для наглядности построены графики (доступен fig):
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.