11.11.2015 Взять и поделить или деление по модулю
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) |
||
| (не показаны 13 промежуточных версий 1 участника) | |||
| Строка 18: | Строка 18: | ||
:'''[c*(a+b)]mod n = [c*a(mod n) + c*b(mod n)]mod n''' | :'''[c*(a+b)]mod n = [c*a(mod n) + c*b(mod n)]mod n''' | ||
| − | Как оказалось, делить можно по-разному, в зависимости от функции, которую мы используем для округления<ref>[https://en.wikipedia.org/wiki/Modulo_operation Wiki: Modulo operation]</ref>: | + | Как оказалось, делить можно по-разному, в зависимости от функции, которую мы используем для округления <ref>[https://en.wikipedia.org/wiki/Modulo_operation Wiki: Modulo operation]</ref>: |
* truncated division modulo - используется функция fix() - округление в сторону нуля, в результате имеем остаток от деления абсолютных значений аргументов, знак используем от первого. | * truncated division modulo - используется функция fix() - округление в сторону нуля, в результате имеем остаток от деления абсолютных значений аргументов, знак используем от первого. | ||
* floored division modulo - используется функция floor() - округление в сторону минус бесконечности, в результате приводим число к интервалу [0 b] для положительных b или [b 0] для отрицательных. | * floored division modulo - используется функция floor() - округление в сторону минус бесконечности, в результате приводим число к интервалу [0 b] для положительных b или [b 0] для отрицательных. | ||
| Строка 141: | Строка 141: | ||
printf("%f %f\n", x, ufmod(x, base)); | printf("%f %f\n", x, ufmod(x, base)); | ||
x += 0.25; | x += 0.25; | ||
| + | } | ||
| + | printf("\n"); | ||
| + | |||
| + | unsigned int ux; | ||
| + | int iy; | ||
| + | unsigned int maxint = (1<<30)-1; // Max positive int 2^31-1 | ||
| + | int halfminint = -(1<<29); // Half of min int | ||
| + | |||
| + | ux = (1<<10) - 1; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<10) - 1; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = maxint; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = maxint; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = 0 - 1; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = 0 - 1; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = 0 - 2; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = 0 - 2; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<30) + 1; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<30) + 1; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<30); iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<30); iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<30) - 1; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<30) - 1; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = 1<<29; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = 1<<29; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<29)-1; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<29)-1; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<29)+1; iy = 13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | ux = (1<<29)+1; iy = -13; | ||
| + | printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy)); | ||
| + | |||
| + | |||
| + | int base = 7; | ||
| + | unsigned int x = 0; | ||
| + | printf("flumod %d \n", base); | ||
| + | while (x < 23) { | ||
| + | printf("%u %d\n", x, flumod(x, base)); | ||
| + | x++; | ||
| + | } | ||
| + | printf("\n"); | ||
| + | |||
| + | base = -7; | ||
| + | x = 0; | ||
| + | printf("flumod %d \n", base); | ||
| + | while (x < 23) { | ||
| + | printf("%u %d\n", x, flumod(x, base)); | ||
| + | x++; | ||
} | } | ||
printf("\n"); | printf("\n"); | ||
| Строка 295: | Строка 379: | ||
|content = | |content = | ||
<center>[[file:20151112_flmod.png]]</center> | <center>[[file:20151112_flmod.png]]</center> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
| + | |||
| + | == Функция flumod(unsigned int, int) == | ||
| + | |||
| + | Функция возвращает floored modulo для пары (unsigned int, int) | ||
| + | |||
| + | {{Hider|title = Исходный код flumod(unsigned int, int) | ||
| + | |content = <source lang="C"> | ||
| + | int flumod(unsigned int x, int y) { | ||
| + | unsigned int maxint = (1<<30)-1; // Max positive int 2^31-1 | ||
| + | int halfminint = -(1<<29); // Half of min int | ||
| + | int intbuf1 = 0; | ||
| + | int intbuf2 = 0; | ||
| + | if (y > 0) { | ||
| + | return x%y; | ||
| + | } else if (y < 0) { | ||
| + | if (x <= maxint) { | ||
| + | return flmod((int)x, y); | ||
| + | } else { | ||
| + | // x = maxint + a | ||
| + | // mod(x, y) = mod( mod(maxint, y) + mod(a, y), y ) | ||
| + | intbuf1 = flumod(maxint, y); | ||
| + | if (intbuf1 < halfminint) // Overflow avoiding | ||
| + | intbuf1 -= y; | ||
| + | intbuf2 = flumod(x - maxint, y); | ||
| + | if (intbuf2 < halfminint) | ||
| + | intbuf2 -= y; | ||
| + | return flmod(intbuf1 + intbuf2, y); | ||
| + | } | ||
| + | } else { | ||
| + | return 0; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
| + | Результаты её выполнения совпадают с MATLAB mod(): | ||
| + | |||
| + | {{Hider|title = flumod(unsigned int, int) | ||
| + | |content = | ||
| + | <center>[[file:20151116_flumod.png]]</center> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
| + | Результаты тестов на большие входные значения: | ||
| + | {{Hider|title = Точечный тест flumod(unsigned int, int) | ||
| + | |content = <source lang="bash"> | ||
| + | flumod(1023, 13) = 9 | ||
| + | flumod(1023, -13) = -4 | ||
| + | flumod(1073741823, 13) = 11 | ||
| + | flumod(1073741823, -13) = -2 | ||
| + | flumod(4294967295, 13) = 8 | ||
| + | flumod(4294967295, -13) = -5 | ||
| + | flumod(4294967294, 13) = 7 | ||
| + | flumod(4294967294, -13) = -6 | ||
| + | flumod(1073741825, 13) = 0 | ||
| + | flumod(1073741825, -13) = 0 | ||
| + | flumod(1073741824, 13) = 12 | ||
| + | flumod(1073741824, -13) = -1 | ||
| + | flumod(1073741823, 13) = 11 | ||
| + | flumod(1073741823, -13) = -2 | ||
| + | flumod(536870912, 13) = 6 | ||
| + | flumod(536870912, -13) = -7 | ||
| + | flumod(536870911, 13) = 5 | ||
| + | flumod(536870911, -13) = -8 | ||
| + | flumod(536870913, 13) = 7 | ||
| + | flumod(536870913, -13) = -6 | ||
| + | </source> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
| + | |||
| + | == Функция flmod2POW32(int) == | ||
| + | |||
| + | Функция возвращает floored modulo для пары (2^32, int) | ||
| + | |||
| + | {{Hider|title = Исходный код flmod2POW32(int) | ||
| + | |content = <source lang="C"> | ||
| + | int flmod2POW32(int base){ | ||
| + | unsigned int ubuf = 0; | ||
| + | if (base > 0) { | ||
| + | ubuf -= base; | ||
| + | return flumod(ubuf, base); | ||
| + | } else if (base < 0) { | ||
| + | ubuf += base; | ||
| + | return flumod(ubuf, base); | ||
| + | } else { | ||
| + | return 0; | ||
| + | } | ||
| + | |||
| + | } | ||
| + | </source> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
| + | |||
| + | Результаты тестов (совпадают с octave): | ||
| + | {{Hider|title = Точечный тест flmod2POW32(int) | ||
| + | |content = <source lang="bash"> | ||
| + | flmod2POW32(1023) = 4 | ||
| + | flmod2POW32(1048575) = 4096 | ||
| + | flmod2POW32(1073741823) = 4 | ||
| + | flmod2POW32(-1073741824) = 0 | ||
| + | flmod2POW32(-1023) = -1019 | ||
| + | flmod2POW32(-1048575) = -1044479 | ||
| + | flmod2POW32(0) = 0 | ||
| + | </source> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
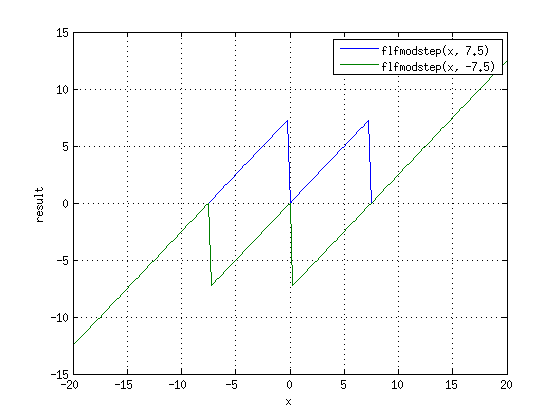
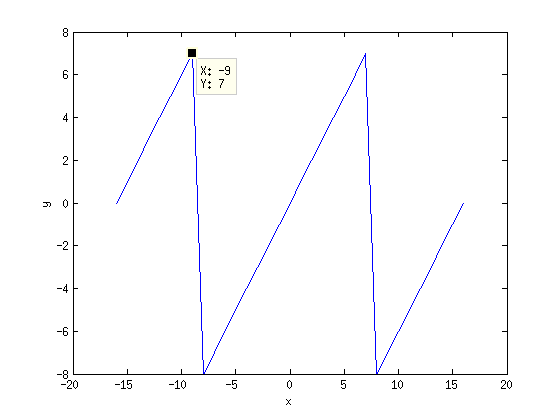
| + | == Функция flfmodstep(double, double) == | ||
| + | |||
| + | При переполнениях возникает задача сделать один шаг операции floored mod, прибавить или удалить только один base | ||
| + | |||
| + | {{Hider|title = flfmodstep(double, double) /доступны fig/ | ||
| + | |content = <source lang="C"> | ||
| + | double flfmodstep(double x, double y){ | ||
| + | if (y > 0) { | ||
| + | if (x < 0) | ||
| + | return x + y; | ||
| + | else { | ||
| + | if (x < y) | ||
| + | return x; | ||
| + | else | ||
| + | return x - y; | ||
| + | } | ||
| + | } else if (y < 0) { | ||
| + | if (x > 0) | ||
| + | return x + y; | ||
| + | else { | ||
| + | if (x > y) | ||
| + | return x; | ||
| + | else | ||
| + | return x - y; | ||
| + | } | ||
| + | } else { | ||
| + | return 0.0; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | <center>[[file:20151113_flfmodstep.png]]</center> | ||
| + | |hidden = 1 | ||
| + | }} | ||
| + | |||
| + | |||
| + | == Симуляция переполнения знакового регистра == | ||
| + | |||
| + | Пусть есть регистр, значение которого интерпретируется как число в доп.коде. Тогда переполнение регистра можно имитировать в MATLAB'е преобразованием: | ||
| + | <source lang="matlab"> | ||
| + | % N - число разрядов регистра | ||
| + | % x - число, которое пытаемся записать в регистр | ||
| + | % y - число, которое окажется в регистре | ||
| + | y = mod(x + 2^(N-1), 2^N) - 2^(N-1); | ||
| + | </source> | ||
| + | |||
| + | {{Hider|title = Имитация переполнения знакового регистра (N = 4) | ||
| + | |content = | ||
| + | <center>[[file:20160212_regoverflow.png]]</center> | ||
|hidden = 1 | |hidden = 1 | ||
}} | }} | ||
Текущая версия на 14:37, 20 мая 2016
|
Есть некоторая неуверенность в результатах работы функций взятия модуля, для борьбы с которой составлена эта памятка.
Лично я привык к работе функции mod(a, b) в MATLAB, которая приводит a к диапазону [0 b] или [b 0] (в зависимости от знака b) путем прибавления/вычитания целого числа b к/из a. Что выражается в формуле:
- mod(a, b) = a - floor(a ./ b)*b,
где функция floor - округление в сторону минус бесконечности.
Операция взятия остатка по модулю замечательна своими свойствами:
- (a+b)mod n = [a(mod n) + b(mod n)]mod n
- (a-b)mod n = [a(mod n) - b(mod n)]mod n
- (a*b)mod n = [a(mod n) * b(mod n)]mod n
- [c*(a+b)]mod n = [c*a(mod n) + c*b(mod n)]mod n
Как оказалось, делить можно по-разному, в зависимости от функции, которую мы используем для округления <ref>Wiki: Modulo operation</ref>:
- truncated division modulo - используется функция fix() - округление в сторону нуля, в результате имеем остаток от деления абсолютных значений аргументов, знак используем от первого.
- floored division modulo - используется функция floor() - округление в сторону минус бесконечности, в результате приводим число к интервалу [0 b] для положительных b или [b 0] для отрицательных.
- и т.д.
Для себя я теперь разделяю понятия остатка от деления (remainder after devision) и приведения числа по модулю (modulus after devision) соответственно.
Как показало исследование ниже, результаты будут отличаться тогда, когда аргументы имеют разный знак.
Так какие функции и операторы реализуют остаток от деления, какие взятие по модулю, и как они зависят от типов аргументов? Ниже представлены результаты, полученные на Oryx 161, компилятор из Xilinx SDK 2014.4 ( gcc version 4.8.3 20140320 (prerelease) (Sourcery CodeBench Lite 2014.05-23)).
int val = 13;
for (i=0; i<sizeof(x)/sizeof(int); i++) {
printf("(int(%d)) %% (int(%d))\t = %d (d)\n", val, x[i], val % x[i]);
}
for (i=0; i<sizeof(x)/sizeof(int); i++) {
printf("(int(%d)) %% (int(%d))\t = %d (d)\n", (-val), x[i], (-val) % x[i]);
}
for (i=0; i<sizeof(x)/sizeof(int); i++) {
printf("(unsigned int(%d)) %% (int(%d)) \t = %d (d)\n", val, x[i], ((unsigned int)val) % x[i]);
}
for (i=4; i<sizeof(x)/sizeof(int); i++) {
printf("(int(%d)) %% (unsigned int(%d)) \t = %d (d)\n", val, x[i], (val) % ((unsigned int)(x[i])));
}
for (i=4; i<sizeof(x)/sizeof(int); i++) {
printf("(int(%d)) %% (unsigned int(%d)) \t = %d (d)\n", -val, x[i], (-val) % ((unsigned int)(x[i])));
}
for (i=4; i<sizeof(x)/sizeof(int); i++) {
printf("(unsigned int(%d)) %% (unsigned int(%d))\t = %d (d)\n", val, x[i], ((unsigned int)val) % ((unsigned int)(x[i])));
}
int base = 7;
int x = -22;
printf("x, x%%%d \n", base);
while (x < 23) {
printf("%d %d\n", x, x%base);
x++;
}
printf("\n");
base = -7;
x = -22;
printf("x, x%%%d \n", base);
while (x < 23) {
printf("%d %d\n", x, x%base);
x++;
}
printf("\n");
base = 7;
x = -22;
printf("x, x%%(u)%d \n", base);
while (x < 23) {
printf("%d %d\n", x, x%((unsigned int)(base)));
x++;
}
printf("\n");
base = -7;
x = 0;
printf("x, (u)x%%%d \n", base);
while (x < 23) {
printf("%d %d\n", x, ((unsigned int)x)%base);
x++;
}
printf("\n");
int base = 7;
int x = -22;
printf("x, flmod(x, %d) \n", base);
while (x < 23) {
printf("%d %d\n", x, flmod(x, base));
x++;
}
printf("\n");
base = -7;
x = -22;
printf("x, flmod(x, %d) \n", base);
while (x < 23) {
printf("%d %d\n", x, flmod(x, base));
x++;
}
printf("\n");
double base = 7.5;
double x = -22.0;
printf("mod(x, %f) \n", base);
while (x < 23.0) {
printf("%f %f\n", x, mod(x, base));
x += 0.25;
}
printf("\n");
base = -7.5;
x = -22.0;
printf("\n", base);
printf("mod(x, %f) \n", base);
while (x < 23.0) {
printf("%f %f\n", x, mod(x, base));
x += 0.25;
}
printf("\n");
double base = 7.5;
double x = -22.0;
printf("ufmod(x, %f) \n", base);
while (x < 23.0) {
printf("%f %f\n", x, ufmod(x, base));
x += 0.25;
}
printf("\n");
base = -7.5;
x = -22.0;
printf("\n", base);
printf("ufmod(x, %f) \n", base);
while (x < 23.0) {
printf("%f %f\n", x, ufmod(x, base));
x += 0.25;
}
printf("\n");
unsigned int ux;
int iy;
unsigned int maxint = (1<<30)-1; // Max positive int 2^31-1
int halfminint = -(1<<29); // Half of min int
ux = (1<<10) - 1; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<10) - 1; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = maxint; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = maxint; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = 0 - 1; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = 0 - 1; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = 0 - 2; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = 0 - 2; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<30) + 1; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<30) + 1; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<30); iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<30); iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<30) - 1; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<30) - 1; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = 1<<29; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = 1<<29; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<29)-1; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<29)-1; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<29)+1; iy = 13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
ux = (1<<29)+1; iy = -13;
printf("flumod(%u, %d) = %d\n", ux, iy, flumod(ux, iy));
int base = 7;
unsigned int x = 0;
printf("flumod %d \n", base);
while (x < 23) {
printf("%u %d\n", x, flumod(x, base));
x++;
}
printf("\n");
base = -7;
x = 0;
printf("flumod %d \n", base);
while (x < 23) {
printf("%u %d\n", x, flumod(x, base));
x++;
}
printf("\n");
exit(0);
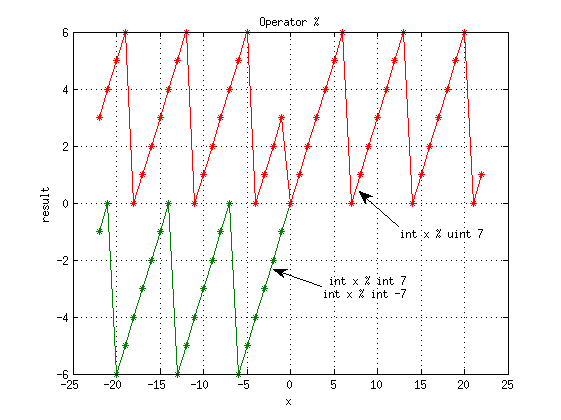
[править] Оператор %
(int(13)) % (int(-7)) = 6
(int(13)) % (int(-5)) = 3
(int(13)) % (int(-1)) = 0
(int(13)) % (int(1)) = 0
(int(13)) % (int(5)) = 3
(int(13)) % (int(7)) = 6
(int(13)) % (int(17)) = 13
(int(-13)) % (int(-17)) = -13
(int(-13)) % (int(-7)) = -6
(int(-13)) % (int(-5)) = -3
(int(-13)) % (int(-1)) = 0
(int(-13)) % (int(1)) = 0
(int(-13)) % (int(5)) = -3
(int(-13)) % (int(7)) = -6
(int(-13)) % (int(17)) = -13
(unsigned int(13)) % (int(-17)) = 13
(unsigned int(13)) % (int(-7)) = 13
(unsigned int(13)) % (int(-5)) = 13
(unsigned int(13)) % (int(-1)) = 13
(unsigned int(13)) % (int(1)) = 0
(unsigned int(13)) % (int(5)) = 3
(unsigned int(13)) % (int(7)) = 6
(unsigned int(13)) % (int(17)) = 13
(int(13)) % (unsigned int(1)) = 0
(int(13)) % (unsigned int(5)) = 3
(int(13)) % (unsigned int(7)) = 6
(int(13)) % (unsigned int(17)) = 13
(int(-13)) % (unsigned int(1)) = 0
(int(-13)) % (unsigned int(5)) = 3
(int(-13)) % (unsigned int(7)) = 5
(int(-13)) % (unsigned int(17)) = 5
(unsigned int(13)) % (unsigned int(1)) = 0
(unsigned int(13)) % (unsigned int(5)) = 3
(unsigned int(13)) % (unsigned int(7)) = 6
(unsigned int(13)) % (unsigned int(17)) = 13
Следует обратить внимание:
- int a % uint b = mod(*(uint*(&a)), b) - результаты для -13%(int 7) и -13%(uint 7) различаются; если брать int % uint, то int интерпретируется как uint, например, -1 превращается в 2^32-1.
- uint a % int b = b<0 ? a : mod(a, b) - взятие uint % отрицательного числа - холостая операция, результат - исходный uint
- int a % int b = sign(a) * mod(|a|, |b|) - как подсказывает стандарт, до C (ISO 1999) и C++ (ISO 2011) знак зависел от реализации, теперь же применяется знак делимого
- int a % int b = (MATLAB)rem(a, b) - ведет себя как функция rem() в MATLAB: rem(a, b) = a - fix(a/b)*b, где fix() - функция округления в сторону нуля
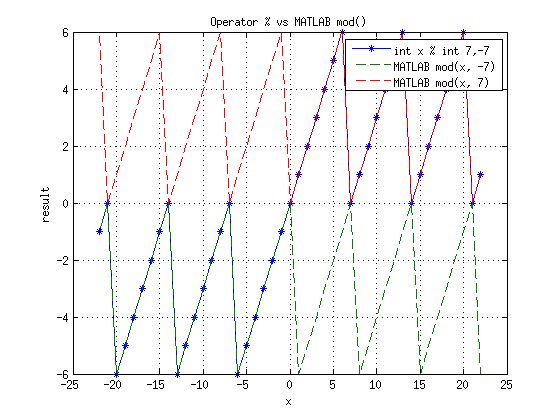
- int a % int b ведет себя как функция mod() в MATLAB только при совпадении знаков аргументов, иначе есть смещение на b (за исключением точек, в которых результат ноль)
Выводы:
- Оператор % дает в нашей системе остаток от деления (truncated division modulo)
- Функция mod() в MATLAB производит floored modulo, функция rem() в MATLAB - truncated modulo.
Для наглядности построены графики (доступен fig):
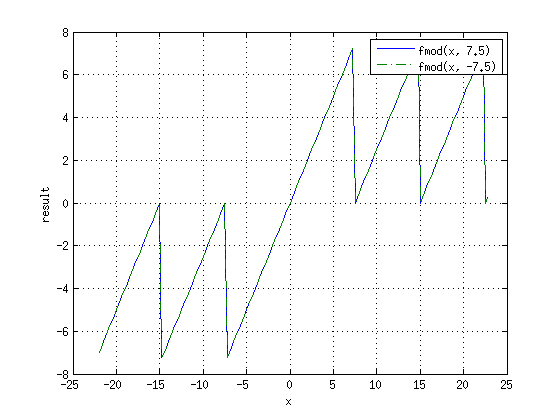
[править] Функция fmod
Функция<ref>http://www.cplusplus.com/reference/cmath/fmod/</ref>:
возвращает остаток от деления в виде числа с плавающей точкой (numer - tquot * denom), где tquot - результат округления в сторону нуля дроби numer/denom. Иначе говоря, функция использует truncated division или функцию fix(). От знака второго аргумента результат не зависит. Буква f в названии функции - отсылка к float, а не floored!
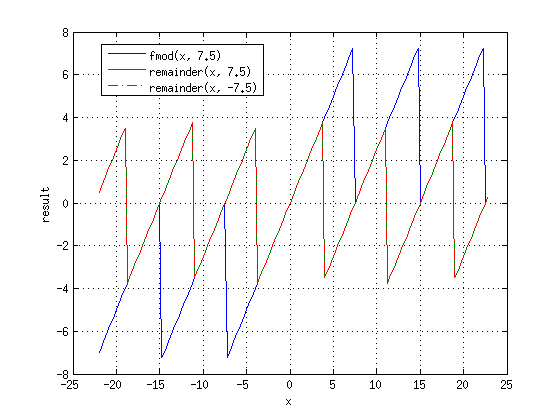
[править] Функция remainder
Функция<ref>http://www.cplusplus.com/reference/cmath/remainder/</ref>:
float remainderf (float numer , float denom);
long double remainderl (long double numer, long double denom);
аналогична fmod(), но использует округление к ближайшему целому, то есть функцию round вместо fix. От знака второго аргумента результат не зависит.
[править] Макрос umod
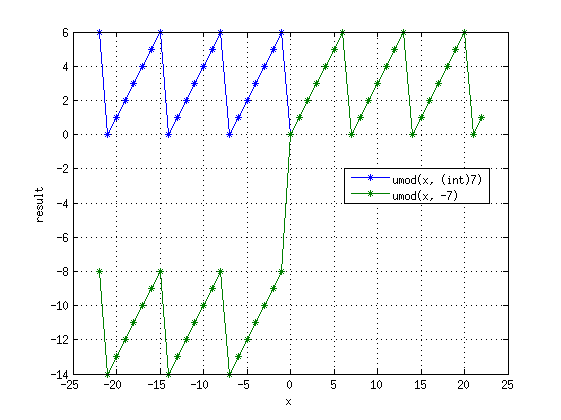
Для имитации matlab'овского mod() для целых чисел у нас существует макрос umod:
При положительных y она работает как и ожидается - реализует floored modulo, при отрицательных есть проблемы.
Кроме того, если в неё мешать использование uint и int, то можно получить интересные эффекты, описанные выше.
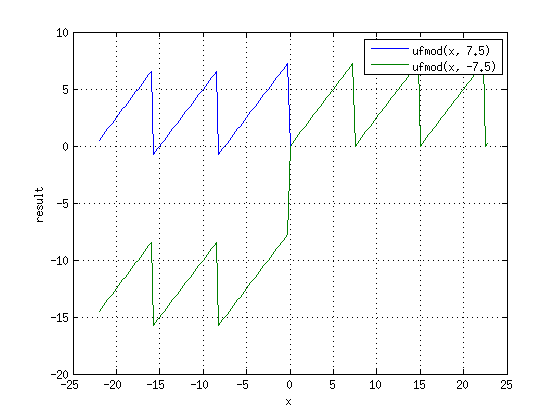
[править] Макрос ufmod
Аналогичен umod, но использовался для чисел типа double. Вызывал ошибки, поэтому сейчас не используется.
Графики показывают, что макрос дает ошибочные значения для отрицательных чисел.
Кроме того, если в неё мешать использование uint и int, то можно получить интересные эффекты, описанные выше.
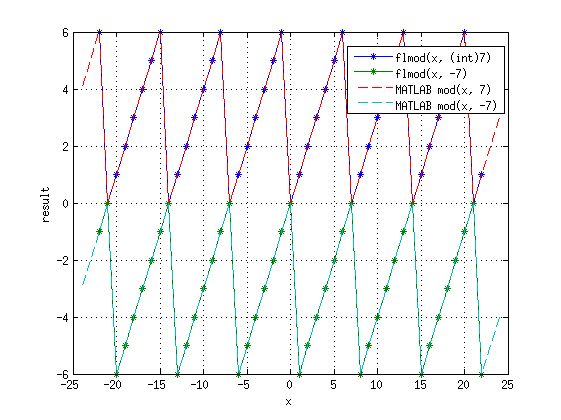
[править] Функция flmod(int, int)
Для исправления недостатков макроса umod создана функция flmod(int, int):
if (y >= 0)
return ( (x>=0) ? (x%y) : (((x+1)%(y))+(y)-1) );
else
return -( (x<=0) ? (-x%-y) : (((-x+1)%(-y))+(-y)-1) );
}
Результаты её выполнения совпадают с MATLAB mod(), она реализует floored modulo:
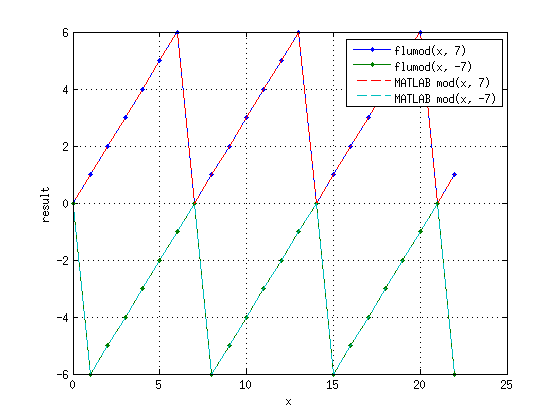
[править] Функция flumod(unsigned int, int)
Функция возвращает floored modulo для пары (unsigned int, int)
unsigned int maxint = (1<<30)-1; // Max positive int 2^31-1
int halfminint = -(1<<29); // Half of min int
int intbuf1 = 0;
int intbuf2 = 0;
if (y > 0) {
return x%y;
} else if (y < 0) {
if (x <= maxint) {
return flmod((int)x, y);
} else {
// x = maxint + a
// mod(x, y) = mod( mod(maxint, y) + mod(a, y), y )
intbuf1 = flumod(maxint, y);
if (intbuf1 < halfminint) // Overflow avoiding
intbuf1 -= y;
intbuf2 = flumod(x - maxint, y);
if (intbuf2 < halfminint)
intbuf2 -= y;
return flmod(intbuf1 + intbuf2, y);
}
} else {
return 0;
}
}
Результаты её выполнения совпадают с MATLAB mod():
Результаты тестов на большие входные значения:
flumod(1023, -13) = -4
flumod(1073741823, 13) = 11
flumod(1073741823, -13) = -2
flumod(4294967295, 13) = 8
flumod(4294967295, -13) = -5
flumod(4294967294, 13) = 7
flumod(4294967294, -13) = -6
flumod(1073741825, 13) = 0
flumod(1073741825, -13) = 0
flumod(1073741824, 13) = 12
flumod(1073741824, -13) = -1
flumod(1073741823, 13) = 11
flumod(1073741823, -13) = -2
flumod(536870912, 13) = 6
flumod(536870912, -13) = -7
flumod(536870911, 13) = 5
flumod(536870911, -13) = -8
flumod(536870913, 13) = 7
flumod(536870913, -13) = -6
[править] Функция flmod2POW32(int)
Функция возвращает floored modulo для пары (2^32, int)
unsigned int ubuf = 0;
if (base > 0) {
ubuf -= base;
return flumod(ubuf, base);
} else if (base < 0) {
ubuf += base;
return flumod(ubuf, base);
} else {
return 0;
}
}
Результаты тестов (совпадают с octave):
flmod2POW32(1048575) = 4096
flmod2POW32(1073741823) = 4
flmod2POW32(-1073741824) = 0
flmod2POW32(-1023) = -1019
flmod2POW32(-1048575) = -1044479
flmod2POW32(0) = 0
[править] Функция flfmodstep(double, double)
При переполнениях возникает задача сделать один шаг операции floored mod, прибавить или удалить только один base
[править] Симуляция переполнения знакового регистра
Пусть есть регистр, значение которого интерпретируется как число в доп.коде. Тогда переполнение регистра можно имитировать в MATLAB'е преобразованием:
% x - число, которое пытаемся записать в регистр
% y - число, которое окажется в регистре
y = mod(x + 2^(N-1), 2^N) - 2^(N-1);
[править] Ссылки
<references/>
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.