16.09.2011, Изучение быстродействия и оптимизация алгоритма БПФ
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) |
||
| Строка 23: | Строка 23: | ||
| [https://code.google.com/p/fft-for-arm-search/source/detail?r=2 2] | | [https://code.google.com/p/fft-for-arm-search/source/detail?r=2 2] | ||
| 23.3 | | 23.3 | ||
| − | | 0. | + | | 0.3 |
| Исходный алгоритм с коэф, вх. и вых. данными во float | | Исходный алгоритм с коэф, вх. и вых. данными во float | ||
|- | |- | ||
| | | | ||
| | | | ||
| − | | 0. | + | | 0.3 |
| Входные данные int: изменений не замечено | | Входные данные int: изменений не замечено | ||
|- | |- | ||
| [https://code.google.com/p/fft-for-arm-search/source/detail?r=3 3] | | [https://code.google.com/p/fft-for-arm-search/source/detail?r=3 3] | ||
| 84.5 | | 84.5 | ||
| − | | | + | | 0.3 |
| Все float переведены в int. Грубая оценка быстродействия целочисленного алгоритма. | | Все float переведены в int. Грубая оценка быстродействия целочисленного алгоритма. | ||
|} | |} | ||
Версия 10:45, 20 сентября 2011
<accesscontrol>SuperUsers</accesscontrol>
Под исходные коды заведен проект fft-for-arm-search.
Исследуется БПФ от 2048 точек.
Согласно изученной литературе, минимальное количество операций достижимо для БПФ размером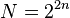 
("четной степени двойки"). Для него:
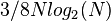- число комплексных умножений;
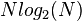- число комплексных сложений.
Остаются два рычага власти: варьировать N и менять разрядность и тип переменных в функции (уменьшать время умножения и сложения).
По произведенным оценкам ARM'у на одно комплексное умножение (float+jfloat)*(float+jfloat) надо около 2.5-2.8 мкс (при расчете пришлось принять гипотезу исчезающе малого влияния суммирования на время вычисления). Отсюда, в изначальном варианте оценка свертки мс-ого сигнала для 10 частот - 300 мс.
| Ревизия | ARM, ms | Pentium, ms | Примечание |
|---|---|---|---|
| 2 | 23.3 | 0.3 | Исходный алгоритм с коэф, вх. и вых. данными во float |
| 0.3 | Входные данные int: изменений не замечено | ||
| 3 | 84.5 | 0.3 | Все float переведены в int. Грубая оценка быстродействия целочисленного алгоритма. |
Бонус
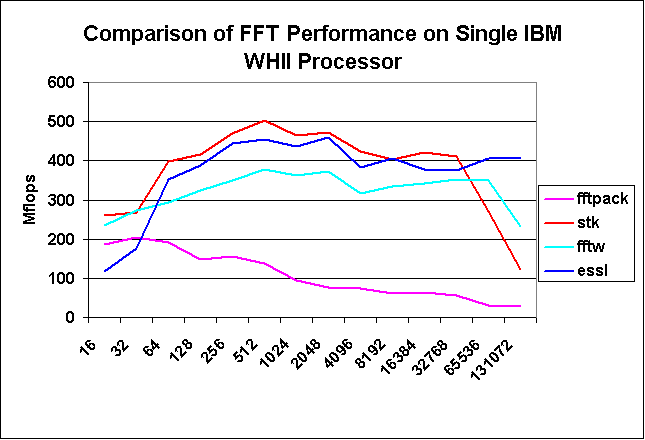
In this figure we compare the performance in MFLOPS of a complex-complex 5*n*log2(n)/t, where n is the length of the sequence and t is the time for one transform. The computations are done on one processor of the IBM Winterhawk II with 375-MHz Power3-II processors. We compare FFTPACK 5 by P. Swarztrauber, NCAR (FFTPACK), the new Spectral Toolkit by Rodney James, NCAR (STK), FFTW by M. Frigio and S. Johnson, MIT (FFTW), and the IBM ESSL Library (ESSL).
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.