Моделирование коррелированных гауссовых СВ — различия между версиями

Версия 14:37, 21 августа 2013

При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции.

Многомерная нормальная СВ или вектор случайных величин?

При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из Википедии:

Случайный вектор 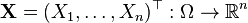$\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n$ имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

Произвольная линейная комбинация компонентов вектора 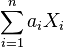$\sum\limits_{i=1}^n a_i X_i$ имеет нормальное распределение или является константой.
Существует вектор независимых стандартных нормальных случайных величин 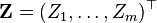$\mathbf{Z}=(Z_1,\ldots, Z_m)^{\top}$ , вещественный вектор 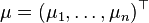$\mathbf{\mu} = (\mu_1,\ldots, \mu_n)^{\top}$ и матрица 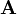$\mathbf{A}$ размерности 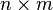$n \times m$ , такие что:

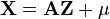$\mathbf{X} = \mathbf{A} \mathbf{Z} + \mathbf{\mu}$ .

Существует вектор 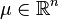$\mathbf{\mu} \in \mathbb{R}^n$ и неотрицательно определённая симметричная матрица 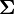$\mathbf{\Sigma}$ размерности 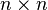$n \times n$ , такие что характеристическая функция вектора 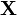$\mathbf{X}$ имеет вид:

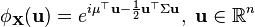$\phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}},\; \mathbf{u} \in \mathbb{R}^n$ .

Версия 14:37, 21 августа 2013 (просмотреть исходный код) Korogodin (обсуждение \| вклад) (→‎Многомерная нормальная СВ или вектор случайных величин?) ← Предыдущая правка		Версия 14:37, 21 августа 2013 (просмотреть исходный код) Korogodin (обсуждение \| вклад) (→‎Многомерная нормальная СВ или вектор случайных величин?) Следующая правка →
Строка 4:		Строка 4:

	При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из [http://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение Википедии]:		При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из [http://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение Википедии]:
		+
	Случайный вектор <math>\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n</math> имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:		Случайный вектор <math>\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n</math> имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

Моделирование коррелированных гауссовых СВ — различия между версиями

Версия 14:37, 21 августа 2013

Многомерная нормальная СВ или вектор случайных величин?

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

SRNS Wiki

Рабочие журналы

Приватный файлсервер

QNAP Сервер

Инструменты