Моделирование коррелированных гауссовых СВ — различия между версиями
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) |
||
| Строка 47: | Строка 47: | ||
Шумы корреляционных сумм <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> получены сворачиванием входного шума <math>n</math> с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> имеет многомерное нормальное распределение (если выборку <math>n</math> обозначить как <math>\mathbf{Z}</math>, опорные сигналы записать в виде трех строк матрицы <math>\mathbf{A}</math>, <math>\mathbf{\mu}</math> - вектор-столбец из трех нулей) | Шумы корреляционных сумм <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> получены сворачиванием входного шума <math>n</math> с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> имеет многомерное нормальное распределение (если выборку <math>n</math> обозначить как <math>\mathbf{Z}</math>, опорные сигналы записать в виде трех строк матрицы <math>\mathbf{A}</math>, <math>\mathbf{\mu}</math> - вектор-столбец из трех нулей) | ||
| − | Итого, <math>n_{Ip} | + | Итого, компоненты <math>D = \left| {\begin{array}{*{20}{c}} |
| + | n_{Ip}&n_{Ie}&n_{Il}\\ | ||
| + | \end{array}} \right|^T</math> образуют многомерную нормальную СВ с нулевым мат. ожиданием и ковариационной матрицей: | ||
<math>D = \left| {\begin{array}{*{20}{c}} | <math>D = \left| {\begin{array}{*{20}{c}} | ||
| − | + | \sigma_{IQ}^2&\rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2&\rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2\\ | |
| − | + | \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2&\sigma_{IQ}^2&\rho \left( \Delta \tau \right) \sigma_{IQ}^2\\ | |
| − | + | \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2&\rho \left( \Delta \tau \right) \sigma_{IQ}^2&\sigma_{IQ}^2 | |
\end{array}} \right|</math> | \end{array}} \right|</math> | ||
[[Category:ММ РУиС (дисциплина)]] | [[Category:ММ РУиС (дисциплина)]] | ||
Версия 11:02, 22 августа 2013
При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции.
Рассмотрим решение данной задачи на примере модели шумов статистического эквивалента корреляционных сумм 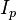 ,
, 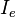 и
и 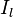 .
.
Статистический эквивалент коррелятора
Статистический эквивалент коррелятора синфазных корреляционных сумм в отсутствии помех можно описать выражениями:
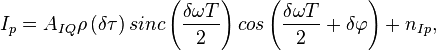
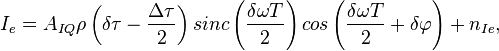
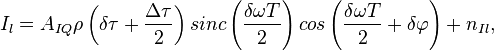
которые для полной картины необходимо дополнить определениями 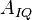 ,
, 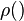 и т.д., а так же описанием шумов
и т.д., а так же описанием шумов 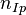 ,
, 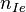 ,
, 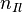 .
.
Математические ожидания СВ 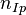 ,
, 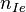 ,
, 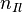 равны нулю, их дисперсии есть
равны нулю, их дисперсии есть
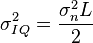 ,
,
где 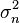 - дисперсия шумов на выходе АЦП,
- дисперсия шумов на выходе АЦП, 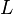 - число суммируемых отсчетов в корреляторе, эти величины считаются известными.
- число суммируемых отсчетов в корреляторе, эти величины считаются известными.
Нетрудно рассчитать попарные взаимные дисперсии:
![M\left[n_{Ip} n_{Ie}\right] = M\left[n_{Ip} n_{Il}\right] = // \frac{\Delta \tau}{2 \tau_e} \sigma_{IQ}^2 // = \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2](/images/math/8/3/7/8373fcc0432a96944c31cd3d9ce8dc3b.png) ,
,
![M\left[n_{Ie} n_{Il}\right] = \rho \left( \Delta \tau \right) \sigma_{IQ}^2](/images/math/7/c/1/7c1993e4fb83239b481e8ede4bba5ee2.png) ,
,
Примечание. Задача формирования шумов квадратурных сумм - абсолютно аналогична и независима, т.к. шумы между I и Q компонентами не коррелируют.
Многомерная нормальная СВ или вектор случайных величин?
При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из Википедии:
Случайный векторимеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:
- Произвольная линейная комбинация компонентов вектора
имеет нормальное распределение или является константой.
- Существует вектор независимых стандартных нормальных случайных величин
, вещественный вектор
и матрица
размерности
, такие что:
.
- Существует вектор
и неотрицательно определённая симметричная матрица
размерности
, такие что характеристическая функция вектора
имеет вид:
.
Из первого условия следует, что каждая из компонент нормальной векторной СВ имеет нормальное распределение (для компоненты 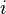 это вытекает при
это вытекает при 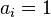 и остальных коэффициентах комбинации, равных 0). Отсюда часто возникает иллюзия, что нормальность распределений компонент влечет нормальность совместного распределения. Этот тезис не выполняется, на контрпример можно взглянуть тут.
и остальных коэффициентах комбинации, равных 0). Отсюда часто возникает иллюзия, что нормальность распределений компонент влечет нормальность совместного распределения. Этот тезис не выполняется, на контрпример можно взглянуть тут.
Шумы корреляционных сумм 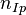 ,
, 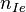 ,
, 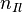 получены сворачиванием входного шума
получены сворачиванием входного шума 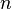 с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка
с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка 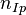 ,
, 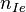 ,
, 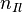 имеет многомерное нормальное распределение (если выборку
имеет многомерное нормальное распределение (если выборку 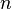 обозначить как
обозначить как 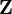 , опорные сигналы записать в виде трех строк матрицы
, опорные сигналы записать в виде трех строк матрицы 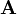 ,
, 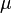 - вектор-столбец из трех нулей)
- вектор-столбец из трех нулей)
Итого, компоненты 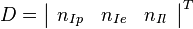 образуют многомерную нормальную СВ с нулевым мат. ожиданием и ковариационной матрицей:
образуют многомерную нормальную СВ с нулевым мат. ожиданием и ковариационной матрицей: