Модель фильтра Калмана 3 порядка — различия между версиями
Материал из SRNS
Korogodin (обсуждение | вклад) (→Листинг) |
Ippolitov (обсуждение | вклад) |
||
| (не показаны 14 промежуточных версий 1 участника) | |||
| Строка 15: | Строка 15: | ||
|category1 = Статистическая радиотехника | |category1 = Статистическая радиотехника | ||
|category2 = Фазовые измерения | |category2 = Фазовые измерения | ||
| − | |category3 = | + | |category3 = |
| − | |category4 = | + | |category4 = Оценивание фазы |
| − | |category5 = | + | |category5 = Оценивание разности фаз |
|category6 = | |category6 = | ||
|category7 = | |category7 = | ||
| Строка 29: | Строка 29: | ||
== Описание модели == | == Описание модели == | ||
| − | Модель фильтра Калмана 3 порядка | + | Модель фильтра Калмана 3 порядка, например, используемого в ФАП. В данный момент приведен листинг только для коэффициентов установившегося режима. Следует привести пример с уравнениями Рикатти. |
| + | |||
| + | == Полоса дискретной следящей системы == | ||
| + | |||
| + | Формула получена адскими страданиями: | ||
| + | <math>H=\frac{4{{K}_{1}}^{2}{{K}_{2}}T-6{{K}_{1}}K_{2}^{2}{{T}^{2}}+7{{K}_{1}}{{K}_{2}}{{K}_{3}}{{T}^{3}}-2{{K}_{1}}K_{3}^{2}{{T}^{4}}-4{{K}_{1}}{{K}_{3}}{{T}^{2}}+4{{K}_{2}}^{2}{{T}^{2}}-4{{K}_{2}}{{K}_{3}}{{T}^{3}}+{{K}_{3}}^{2}{{T}^{4}}}{\left( {{K}_{1}}{{K}_{2}}T-{{K}_{3}}{{T}^{2}} \right)\left( {{K}_{3}}{{T}^{2}}-2{{K}_{2}}T-4{{K}_{1}}+8 \right)\cdot 2\cdot T}</math> | ||
| + | |||
| + | Чтобы получить выражение для второго порядка, следует обнулить лишний коэффициент. | ||
== Листинг == | == Листинг == | ||
| − | Ниже приведен листинг при | + | Ниже приведен листинг при использовании коэффициентов установившегося режима. Изложение следует дополнить уравнениями Рикатти - для честного соответствия заголовку. |
[[File:20110520_K2K3.png|thumb|Коэффициенты передачи непрерывных следящих систем второго и третьего порядка]] | [[File:20110520_K2K3.png|thumb|Коэффициенты передачи непрерывных следящих систем второго и третьего порядка]] | ||
| Строка 42: | Строка 49: | ||
C = fix(Tmod/Tc); | C = fix(Tmod/Tc); | ||
| − | |||
Xextr = [0; 0; 0]; % Вектор экстраполяций | Xextr = [0; 0; 0]; % Вектор экстраполяций | ||
| Строка 58: | Строка 64: | ||
K = K*Tc; % Переход к коэффициентам дискретной системы | K = K*Tc; % Переход к коэффициентам дискретной системы | ||
| + | Xist = [0; 0; 0]; % Истинный вектор состояния | ||
| + | stdIst = 10; nIst = randn(1,C); | ||
for c = 1:C | for c = 1:C | ||
| − | + | Ud = f(Xextr, Xist); % Дискриминатор | |
| − | end | + | Sd = f(A_IQ); % Крутизна дискриминационной характеристики |
| + | Xest = Xextr + K*Ud/Sd; % Вектор оценок на c-й интервал | ||
| + | Xextr = F*Xest; % Экстраполяция на интервал c+1 | ||
| + | |||
| + | Xist = F*Xist + [0; 0; 1]*nIst(c)*stdIst; % Здесь может быть любая другая модель изменения истинного вектора состояния | ||
| + | end | ||
</source> | </source> | ||
Текущая версия на 17:03, 22 июля 2016
| Описание | Модель фильтра Калмана 3 порядка на примере ФАП |
| Автор(ы) | Korogodin (Korogodinобсуждение) |
| Последняя версия | 1.0 (20.05.2011) |
| Загрузить | no link |
| Хранилище | no link |
| Категории | Статистическая радиотехника, Фазовые измерения, Оценивание фазы, Оценивание разности фаз |
Содержание |
[править] Описание модели
Модель фильтра Калмана 3 порядка, например, используемого в ФАП. В данный момент приведен листинг только для коэффициентов установившегося режима. Следует привести пример с уравнениями Рикатти.
[править] Полоса дискретной следящей системы
Формула получена адскими страданиями:
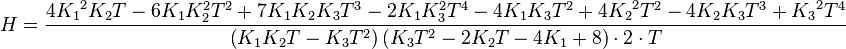
Чтобы получить выражение для второго порядка, следует обнулить лишний коэффициент.
[править] Листинг
Ниже приведен листинг при использовании коэффициентов установившегося режима. Изложение следует дополнить уравнениями Рикатти - для честного соответствия заголовку.
Tmod = 300; % Время моделирования
Tc = 0.005; % Период работы фильтров
C = fix(Tmod/Tc);
Xextr = [0; 0; 0]; % Вектор экстраполяций
F = [1 Tc Tc^2/2;
0 1 Tc;
0 0 1 ]; % Переходная матрица
H = 20; % Hz, полоса
K = nan(3,1); % Вектор-столбец коэффициентов фильтра
K(3) = (1.2*H)^3; % Коэффициенты непрерывной системы в установившемся режиме
K(2) = 2*(K(3))^(2/3);
K(1) = 2*(K(3))^(1/3);
K = K*Tc; % Переход к коэффициентам дискретной системы
Xist = [0; 0; 0]; % Истинный вектор состояния
stdIst = 10; nIst = randn(1,C);
for c = 1:C
Ud = f(Xextr, Xist); % Дискриминатор
Sd = f(A_IQ); % Крутизна дискриминационной характеристики
Xest = Xextr + K*Ud/Sd; % Вектор оценок на c-й интервал
Xextr = F*Xest; % Экстраполяция на интервал c+1
Xist = F*Xist + [0; 0; 1]*nIst(c)*stdIst; % Здесь может быть любая другая модель изменения истинного вектора состояния
end
Tc = 0.005; % Период работы фильтров
C = fix(Tmod/Tc);
Xextr = [0; 0; 0]; % Вектор экстраполяций
F = [1 Tc Tc^2/2;
0 1 Tc;
0 0 1 ]; % Переходная матрица
H = 20; % Hz, полоса
K = nan(3,1); % Вектор-столбец коэффициентов фильтра
K(3) = (1.2*H)^3; % Коэффициенты непрерывной системы в установившемся режиме
K(2) = 2*(K(3))^(2/3);
K(1) = 2*(K(3))^(1/3);
K = K*Tc; % Переход к коэффициентам дискретной системы
Xist = [0; 0; 0]; % Истинный вектор состояния
stdIst = 10; nIst = randn(1,C);
for c = 1:C
Ud = f(Xextr, Xist); % Дискриминатор
Sd = f(A_IQ); % Крутизна дискриминационной характеристики
Xest = Xextr + K*Ud/Sd; % Вектор оценок на c-й интервал
Xextr = F*Xest; % Экстраполяция на интервал c+1
Xist = F*Xist + [0; 0; 1]*nIst(c)*stdIst; % Здесь может быть любая другая модель изменения истинного вектора состояния
end
