Моделирование коррелированных гауссовых СВ — различия между версиями
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) (→Многомерная нормальная СВ или вектор случайных величин?) |
||
| (не показаны 25 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции. | При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции. | ||
| − | + | Рассмотрим решение данной задачи на примере модели шумов статистического эквивалента корреляционных сумм <math>I_p</math>, <math>I_e</math> и <math>I_l</math>. | |
| − | + | == Статистический эквивалент коррелятора == | |
| − | Определение из [http://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение Википедии]: | + | Статистический эквивалент коррелятора синфазных корреляционных сумм в отсутствии помех можно описать выражениями: |
| + | |||
| + | <math>I_p = A_{IQ} \rho\left(\delta \tau\right) sinc\left(\frac{\delta \omega T}{2}\right) cos\left(\frac {\delta \omega T}{2} + \delta\varphi\right) + n_{Ip},</math> | ||
| + | |||
| + | <math>I_{e} = A_{IQ} \rho\left(\delta \tau - \frac{\Delta \tau}{2}\right) sinc\left(\frac{\delta \omega T}{2}\right) cos\left(\frac {\delta \omega T}{2} + \delta\varphi\right) + n_{Ie},</math> | ||
| + | |||
| + | <math>I_{l} = A_{IQ} \rho\left(\delta \tau + \frac{\Delta \tau}{2}\right) sinc\left(\frac{\delta \omega T}{2}\right) cos\left(\frac {\delta \omega T}{2} + \delta\varphi\right) + n_{Il},</math> | ||
| + | |||
| + | которые для полной картины необходимо дополнить определениями <math>A_{IQ}</math>, <math>\rho()</math> и т.д., а так же описанием шумов <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math>. | ||
| + | |||
| + | Математические ожидания СВ <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> равны нулю, их дисперсии есть | ||
| + | |||
| + | <math>\sigma_{IQ}^2 = \frac{\sigma_n^2 N}{2}</math>, | ||
| + | |||
| + | где <math>\sigma_n^2</math> - дисперсия шумов на выходе АЦП, <math>N</math> - число суммируемых отсчетов в корреляторе, эти величины считаются известными. | ||
| + | |||
| + | Нетрудно рассчитать попарные взаимные дисперсии: | ||
| + | |||
| + | <math>M\left[n_{Ip} n_{Ie}\right] = M\left[n_{Ip} n_{Il}\right] = \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2</math>, | ||
| + | |||
| + | <math>M\left[n_{Ie} n_{Il}\right] = \rho \left( \Delta \tau \right) \sigma_{IQ}^2</math>, | ||
| + | |||
| + | Требуется на ЭВМ, имея генератор случайных нормальных чисел, '''формировать реализации СВ''' <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math>. | ||
| + | |||
| + | ''Примечание.'' Задача формирования шумов квадратурных сумм - абсолютно аналогична и независима, т.к. шумы между I и Q компонентами не коррелируют и независимы. | ||
| + | |||
| + | == Многомерная нормальная СВ или вектор случайных величин? == | ||
| + | |||
| + | При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из [http://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение Википедии]: | ||
| + | <blockquote> | ||
Случайный вектор <math>\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n</math> имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий: | Случайный вектор <math>\mathbf{X} = (X_1,\ldots, X_n)^{\top}: \Omega \to \mathbb{R}^n</math> имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий: | ||
| Строка 14: | Строка 43: | ||
* Существует вектор <math>\mathbf{\mu} \in \mathbb{R}^n</math> и неотрицательно определённая симметричная матрица <math>\mathbf{\Sigma}</math> размерности <math>n \times n</math>, такие что характеристическая функция вектора <math>\mathbf{X}</math> имеет вид: | * Существует вектор <math>\mathbf{\mu} \in \mathbb{R}^n</math> и неотрицательно определённая симметричная матрица <math>\mathbf{\Sigma}</math> размерности <math>n \times n</math>, такие что характеристическая функция вектора <math>\mathbf{X}</math> имеет вид: | ||
: <math>\phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}},\; \mathbf{u} \in \mathbb{R}^n</math>. | : <math>\phi_{\mathbf{X}}(\mathbf{u}) = e^{i \mathbf{\mu}^{\top} \mathbf{u} - \frac{1}{2}\mathbf{u}^{\top} \Sigma \mathbf{u}},\; \mathbf{u} \in \mathbb{R}^n</math>. | ||
| + | </blockquote> | ||
| + | |||
| + | Из первого условия следует, что каждая из компонент нормальной векторной СВ имеет нормальное распределение (для компоненты <math>i</math> это вытекает при <math>a_i = 1</math> и остальных коэффициентах комбинации, равных 0). Отсюда часто возникает иллюзия, что нормальность распределений компонент влечет нормальность совместного распределения. Этот тезис не выполняется, на контрпример можно взглянуть [http://risktheory.ru/topic_normmarg.htm тут]. | ||
| + | |||
| + | Шумы корреляционных сумм <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> получены сворачиванием входного шума <math>n</math> с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка <math>n_{Ip}</math>, <math>n_{Ie}</math>, <math>n_{Il}</math> '''имеет многомерное нормальное распределение''' (если выборку <math>n</math> обозначить как <math>\mathbf{Z}</math>, опорные сигналы записать в виде трех строк матрицы <math>\mathbf{A}</math>, <math>\mathbf{\mu}</math> - вектор-столбец из трех нулей) | ||
| + | |||
| + | Итого, компоненты <math>\left| {\begin{array}{*{20}{c}} | ||
| + | n_{Ip}&n_{Ie}&n_{Il}\\ | ||
| + | \end{array}} \right|^T</math> образуют многомерную нормальную СВ с нулевым мат. ожиданием и ковариационной матрицей: | ||
| + | |||
| + | <math>D = \left| {\begin{array}{*{20}{c}} | ||
| + | \sigma_{IQ}^2&\rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2&\rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2\\ | ||
| + | \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2&\sigma_{IQ}^2&\rho \left( \Delta \tau \right) \sigma_{IQ}^2\\ | ||
| + | \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2&\rho \left( \Delta \tau \right) \sigma_{IQ}^2&\sigma_{IQ}^2 | ||
| + | \end{array}} \right|</math>. | ||
| + | |||
| + | == Разложение Холецкого == | ||
| + | |||
| + | Существует разложение матрицы <math>A</math> в виде <math>A = LL^T</math>, где <math>L</math> — нижняя треугольная матрица со строго положительными элементами на диагонали. Данное представление называется [http://ru.wikipedia.org/wiki/Разложение_Холецкого разложением Холецкого] и относительно легко рассчитывается. Разложение Холецкого всегда существует и единственно для любой симметричной положительно-определённой матрицы. | ||
| + | |||
| + | Применим разложение Холецкого к ковариационной матрице: | ||
| + | |||
| + | <math>L = chol(D), D = LL^T</math>. | ||
| + | |||
| + | Умножим полученную матрицу на вектор-столбец <math>r</math> из трех независимых нормальных стандартных СВ: | ||
| + | |||
| + | <math>n_I = L r</math>. | ||
| + | |||
| + | Компоненты вектора <math>n_I</math> образуют многомерную нормальную случайную величину, т.к. выполняется второе необходимое и достаточное условие. | ||
| + | |||
| + | Нетрудно показать, что вектор математических ожиданий <math>n_I</math> - нулевой, а ковариационная матрица <math>D = LL^T</math>. Таким образом, <math>n_I</math> - требуемая многомерная СВ. | ||
| + | |||
| + | == Реализация в MATLAB == | ||
| + | |||
| + | Пример использования: | ||
| + | <source lang="matlab"> | ||
| + | qcno_dB = 45; | ||
| + | N = 10000; | ||
| + | stdn = 8; | ||
| + | |||
| + | stdn_IQ = sqrt(stdn^2 * N /2); | ||
| + | |||
| + | ro1 = 0.75; | ||
| + | ro2 = 0.5; | ||
| + | Dp=stdn_IQ^2; Dpe=ro1*stdn_IQ^2; Del=ro2*stdn_IQ^2; | ||
| + | |||
| + | L=chol([Dp Dpe Dpe; | ||
| + | Dpe Dp Del; | ||
| + | Dpe Del Dp])'; | ||
| + | |||
| + | Nj = 1000000; | ||
| + | nIp = nan(1,Nj); | ||
| + | nIe = nan(1,Nj); | ||
| + | nIl = nan(1,Nj); | ||
| + | for j = 1:Nj | ||
| + | nI = L*randn(3,1); | ||
| + | |||
| + | nIp(j) = nI(1); | ||
| + | nIe(j) = nI(2); | ||
| + | nIl(j) = nI(3); | ||
| + | end | ||
| + | |||
| + | fprintf('Corrcoeff nIp nIe = %f\n', mean(nIp.*nIe / std(nIp) / std(nIe) )); | ||
| + | fprintf('Corrcoeff nIl nIe = %f\n', mean(nIl.*nIe / std(nIl) / std(nIe) )); | ||
| + | </source> | ||
| + | |||
| + | Вывод: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | Corrcoeff nIp nIe = 0.750737 | ||
| + | Corrcoeff nIl nIe = 0.500801 | ||
| + | </source> | ||
| + | |||
| + | Реализация в виде функции (не стоит использовать в цикле, т.к. каждый раз будет вычисляться разложение): | ||
| + | <source lang="matlab"> | ||
| + | |||
| + | function [X, L] = getCorrelatedRV( D, m ) | ||
| + | %GETCORRELATEDRV Returns gaussian corralated random vector | ||
| + | |||
| + | sizeD = size(D); | ||
| + | |||
| + | if (sizeD(1) ~= sizeD(2)) | ||
| + | error('Covariance matrix must be square.') | ||
| + | end | ||
| + | |||
| + | if (nargin == 1) | ||
| + | m = zeros(sizeD(1), 1); | ||
| + | elseif ((nargin < 1) || (nargin > 2)) | ||
| + | error('Incorrect number of inputs.'); | ||
| + | end | ||
| + | |||
| + | if nargin == 2 | ||
| + | sizem = size(m); | ||
| + | if sizem(1) == 1 | ||
| + | m = m'; | ||
| + | sizem = size(m); | ||
| + | end | ||
| + | if sizem(2) > 1 | ||
| + | error('Second argument must be vector.'); | ||
| + | end | ||
| + | if (sizem(1) ~= sizeD(1)) | ||
| + | error('Dimensions of D and m are not consistent.'); | ||
| + | end | ||
| + | end | ||
| + | |||
| + | L = chol(D)'; | ||
| + | |||
| + | X = L * randn(sizeD(1), 1) + m; | ||
| + | |||
| + | end | ||
| + | </source> | ||
[[Category:ММ РУиС (дисциплина)]] | [[Category:ММ РУиС (дисциплина)]] | ||
| + | [[Category:Моделирование]] | ||
Текущая версия на 14:56, 8 мая 2014
При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции.
Рассмотрим решение данной задачи на примере модели шумов статистического эквивалента корреляционных сумм 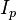 ,
, 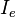 и
и 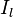 .
.
Содержание |
[править] Статистический эквивалент коррелятора
Статистический эквивалент коррелятора синфазных корреляционных сумм в отсутствии помех можно описать выражениями:
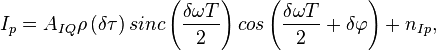
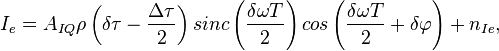
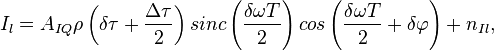
которые для полной картины необходимо дополнить определениями 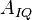 ,
, 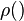 и т.д., а так же описанием шумов
и т.д., а так же описанием шумов 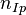 ,
, 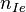 ,
, 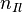 .
.
Математические ожидания СВ 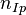 ,
, 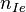 ,
, 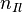 равны нулю, их дисперсии есть
равны нулю, их дисперсии есть
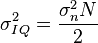 ,
,
где 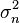 - дисперсия шумов на выходе АЦП,
- дисперсия шумов на выходе АЦП, 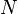 - число суммируемых отсчетов в корреляторе, эти величины считаются известными.
- число суммируемых отсчетов в корреляторе, эти величины считаются известными.
Нетрудно рассчитать попарные взаимные дисперсии:
![M\left[n_{Ip} n_{Ie}\right] = M\left[n_{Ip} n_{Il}\right] = \rho \left( \frac{\Delta \tau}{2} \right) \sigma_{IQ}^2](/images/math/a/0/8/a08e54996eb6a37186e752abd5a70b90.png) ,
,
![M\left[n_{Ie} n_{Il}\right] = \rho \left( \Delta \tau \right) \sigma_{IQ}^2](/images/math/7/c/1/7c1993e4fb83239b481e8ede4bba5ee2.png) ,
,
Требуется на ЭВМ, имея генератор случайных нормальных чисел, формировать реализации СВ 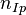 ,
, 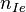 ,
, 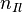 .
.
Примечание. Задача формирования шумов квадратурных сумм - абсолютно аналогична и независима, т.к. шумы между I и Q компонентами не коррелируют и независимы.
[править] Многомерная нормальная СВ или вектор случайных величин?
При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из Википедии:
Случайный векторимеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:
- Произвольная линейная комбинация компонентов вектора
имеет нормальное распределение или является константой.
- Существует вектор независимых стандартных нормальных случайных величин
, вещественный вектор
и матрица
размерности
, такие что:
.
- Существует вектор
и неотрицательно определённая симметричная матрица
размерности
, такие что характеристическая функция вектора
имеет вид:
.
Из первого условия следует, что каждая из компонент нормальной векторной СВ имеет нормальное распределение (для компоненты 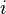 это вытекает при
это вытекает при 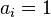 и остальных коэффициентах комбинации, равных 0). Отсюда часто возникает иллюзия, что нормальность распределений компонент влечет нормальность совместного распределения. Этот тезис не выполняется, на контрпример можно взглянуть тут.
и остальных коэффициентах комбинации, равных 0). Отсюда часто возникает иллюзия, что нормальность распределений компонент влечет нормальность совместного распределения. Этот тезис не выполняется, на контрпример можно взглянуть тут.
Шумы корреляционных сумм 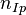 ,
, 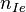 ,
, 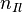 получены сворачиванием входного шума
получены сворачиванием входного шума 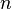 с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка
с тремя опорными сигналами. Таким образом, выполняется второе необходимое и достаточное условие того, что тройка 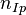 ,
, 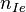 ,
, 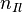 имеет многомерное нормальное распределение (если выборку
имеет многомерное нормальное распределение (если выборку 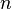 обозначить как
обозначить как 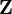 , опорные сигналы записать в виде трех строк матрицы
, опорные сигналы записать в виде трех строк матрицы 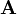 ,
, 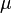 - вектор-столбец из трех нулей)
- вектор-столбец из трех нулей)
Итого, компоненты 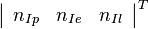 образуют многомерную нормальную СВ с нулевым мат. ожиданием и ковариационной матрицей:
образуют многомерную нормальную СВ с нулевым мат. ожиданием и ковариационной матрицей:
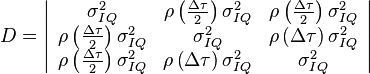 .
.
[править] Разложение Холецкого
Существует разложение матрицы 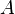 в виде
в виде 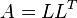 , где
, где 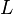 — нижняя треугольная матрица со строго положительными элементами на диагонали. Данное представление называется разложением Холецкого и относительно легко рассчитывается. Разложение Холецкого всегда существует и единственно для любой симметричной положительно-определённой матрицы.
— нижняя треугольная матрица со строго положительными элементами на диагонали. Данное представление называется разложением Холецкого и относительно легко рассчитывается. Разложение Холецкого всегда существует и единственно для любой симметричной положительно-определённой матрицы.
Применим разложение Холецкого к ковариационной матрице:
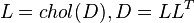 .
.
Умножим полученную матрицу на вектор-столбец  из трех независимых нормальных стандартных СВ:
из трех независимых нормальных стандартных СВ:
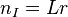 .
.
Компоненты вектора 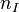 образуют многомерную нормальную случайную величину, т.к. выполняется второе необходимое и достаточное условие.
образуют многомерную нормальную случайную величину, т.к. выполняется второе необходимое и достаточное условие.
Нетрудно показать, что вектор математических ожиданий 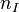 - нулевой, а ковариационная матрица
- нулевой, а ковариационная матрица 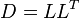 . Таким образом,
. Таким образом, 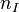 - требуемая многомерная СВ.
- требуемая многомерная СВ.
[править] Реализация в MATLAB
Пример использования:
N = 10000;
stdn = 8;
stdn_IQ = sqrt(stdn^2 * N /2);
ro1 = 0.75;
ro2 = 0.5;
Dp=stdn_IQ^2; Dpe=ro1*stdn_IQ^2; Del=ro2*stdn_IQ^2;
L=chol([Dp Dpe Dpe;
Dpe Dp Del;
Dpe Del Dp])';
Nj = 1000000;
nIp = nan(1,Nj);
nIe = nan(1,Nj);
nIl = nan(1,Nj);
for j = 1:Nj
nI = L*randn(3,1);
nIp(j) = nI(1);
nIe(j) = nI(2);
nIl(j) = nI(3);
end
fprintf('Corrcoeff nIp nIe = %f\n', mean(nIp.*nIe / std(nIp) / std(nIe) ));
fprintf('Corrcoeff nIl nIe = %f\n', mean(nIl.*nIe / std(nIl) / std(nIe) ));
Вывод:
Corrcoeff nIl nIe = 0.500801
Реализация в виде функции (не стоит использовать в цикле, т.к. каждый раз будет вычисляться разложение):
%GETCORRELATEDRV Returns gaussian corralated random vector
sizeD = size(D);
if (sizeD(1) ~= sizeD(2))
error('Covariance matrix must be square.')
end
if (nargin == 1)
m = zeros(sizeD(1), 1);
elseif ((nargin < 1) || (nargin > 2))
error('Incorrect number of inputs.');
end
if nargin == 2
sizem = size(m);
if sizem(1) == 1
m = m';
sizem = size(m);
end
if sizem(2) > 1
error('Second argument must be vector.');
end
if (sizem(1) ~= sizeD(1))
error('Dimensions of D and m are not consistent.');
end
end
L = chol(D)';
X = L * randn(sizeD(1), 1) + m;
end