Владимир Днепров (переписка) — различия между версиями

Версия 21:42, 2 марта 2012

02 мартра 2012, Вероятность ложной тревоги

На данном этапе ты задачу можно сформулировать следующим образом: "Определить зависимость вероятности ложной тревоги схемы обнаружения сигнала от:

порога;
отношения сигнал/шум;
числа некогерентных накоплений."

Более подробно можно прочесть в книгах и тут. Кратко ниже.

Что же это за схема такая, "обнаружения сигнала". Это схема, которая после наблюдения на некотором интервале времени выборки с АЦП, даёт заключение - есть сигнал в данной выборке или всё же нет его. В терминах теории оптимальной фильтрации это означает оценить параметр 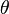$\theta$ для наблюдений вида:

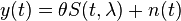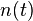$y(t) = \theta S(t, \lambda) + n(t)$ , где $t=[0, T]$ , $n(t)$ - АБГШ с известными параметрами, 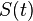$S(t)$ - известный тебе сигнал с параметрами 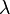$\lambda$ (известными или не известными заранее).

В случае, если в сигнале тебе не известна только начальная фаза, то оптимальным (по некоторому критерию) является алгоритм, схема которого приведена на 105 странице учебника, рис. 4.9. При этом корень брать не обязательно. Выход этой схемы сравнивается с порогом, если порог превышен - значит оценка 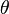$\theta$ становится единицей.

Обрати внимание на структуру схемы. В ней, как и практически всегда при АБГШ, возникает коррелятор (два канала - синфазный и квадратурный, в наших обозначениях I и Q).

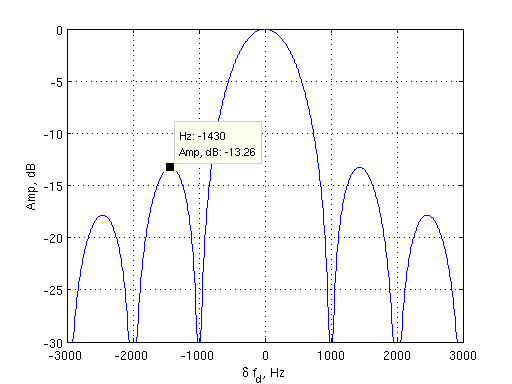
В реальности частоту мы не знаем, поэтому схему приходится немного модифицировать. Неточное значение частоты приводит к уменьшению уровня сигнала при увеличении времени накопления (интегрирования). Копят когерентно от 1 до 10 мс, а затем выход схемы (без корня) начинают просто суммировать. Например, прокопили (проинтегрировали раздельно) честно 5 мс, взяли 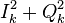$I_k^2 + Q_k^2$ (на схеме это 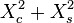$X_c^2 + X_s^2$ ), закинули результат в аккумулятор, далее ещё раз посчитали квадратуры, опять взяли квадраты (что есть амплитуда в квадрате), закинули в аккумулятор и т.д. Это так называемое некогерентное накопление, в противоположность когерентному накоплению в каналах коррелятора. В одном случае происходит векторное накопление (сложение) вектора сигнала, в другом суммирование его модуля. 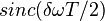Когерентное более выгодно в смысле отношения полезной составляющей к шумовой, но в нём "просаживается" полезная составляющая при наличии ошибки по частоте как $sinc(\delta\omega T/2)$ .

Схема получается такая:

Распределение на выходе схемы - Хи-квадрат.

На данном этапе мы рассматриваем ситуацию, когда сигнала нет. Соответственно чем больше ты берешь порог, тем меньше площадь под кривой справа, тем ниже вероятность превышения порога, ниже вероятность ложной тревоги.

Поэтому ты запускаешь схему без сигнала Np раз, считаешь число np превышений порога, а далее используешь 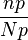$\frac{np}{Np}$ как оценку вероятности данного события при данных параметрах.

@@ Строка 22: / Строка 22: @@
 Схема получается такая:
 [[File:20120302_Неког.png|center]]
+Распределение на выходе схемы - Хи-квадрат.
+На данном этапе мы рассматриваем ситуацию, когда '''сигнала нет'''. Соответственно чем больше ты берешь порог, тем меньше площадь под кривой справа, тем ниже вероятность превышения порога, ниже вероятность '''ложной тревоги'''.
+Поэтому ты запускаешь схему без сигнала Np раз, считаешь число np превышений порога, а далее используешь <math>\frac{np}{Np}</math> как оценку вероятности данного события при данных параметрах.

Владимир Днепров (переписка) — различия между версиями

Версия 21:42, 2 марта 2012

02 мартра 2012, Вероятность ложной тревоги

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

SRNS Wiki

Рабочие журналы

Приватный файлсервер

QNAP Сервер

Инструменты