03.06.2011, Алгоритм оценки задержки аналоговых частей в случае трех антенн

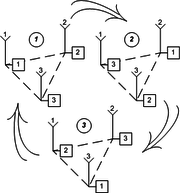
Необходимо обобщить результаты, полученные для коммутации двух антенн на случай коммутации трех антенн. Учесть неоднородность задержек в коммутаторе.

Круговорот аналоговых частей в природе

Сборочный чертеж антенного коммутатор

Рукопись: формирование измерений разности фаз с учетом неоднородности задержек коммутатора и аналоговых частей

Попытка 1

Модель измерений разности фаз

Для измерений разности фаз можно записать следующую модель:

• в фазе 1 циклограммы:

$\psi_{21,izm} = \psi_{21} + \Delta_{21} + \chi_{25} - \chi_{14};$

$\psi_{31,izm} = \psi_{31} + \Delta_{31} + \chi_{36} - \chi_{14};$

• в фазе 2 циклограммы:

$\psi_{21,izm} = \psi_{21} - \Delta_{31} + \chi_{24} - \chi_{16};$

$\psi_{31,izm} = \psi_{31} + \Delta_{21} - \Delta_{31} + \chi_{35} - \chi_{16};$

• в фазе 3 циклограммы:

$\psi_{21,izm} = \psi_{21} + \Delta_{31} - \Delta_{21} + \chi_{26} - \chi_{15};$

$\psi_{31,izm} = \psi_{31} - \Delta_{21} + \chi_{34} - \chi_{15},$

где

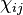$\chi_{ij}$ - задержка с i-го на j-й порт коммутатора,

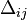$\Delta_{ij}$ - разность задержек i-ой и j-ой аналоговых частей,

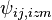$\psi_{ij,izm}$ - измеренная первая разность фаз i-ой и j-ой приемной точки,

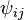$\psi_{ij}$ - истинная первая разность фаз i-ой и j-ой приемной точки.

Дополнительный вектор состояния

Как видно из модели измерений разности фаз, для получения истинных первых разностей из измеренных достаточно оценить шесть параметров:

• в фазе 1 циклограммы:

$\gamma_{21,1} = \Delta_{21} + \chi_{25} - \chi_{14};$

$\gamma_{31,1} = \Delta_{31} + \chi_{36} - \chi_{14};$

• в фазе 2 циклограммы:

$\gamma_{21,2} = - \Delta_{31} + \chi_{24} - \chi_{16};$

$\gamma_{31,2} = \Delta_{21} - \Delta_{31} + \chi_{35} - \chi_{16};$

• в фазе 3 циклограммы:

$\gamma_{21,3} = \Delta_{31} - \Delta_{21} + \chi_{26} - \chi_{15};$

$\gamma_{31,3} = - \Delta_{21} + \chi_{34} - \chi_{15}.$

Соберем из них вектор состояния для будущего фильтра:

$\mathbf{x}_{\gamma }^{{}}=\left| \begin{matrix} \gamma _{21,1}^{{}} & \gamma _{31,1}^{{}} & \gamma _{21,2}^{{}} & \gamma _{31,2}^{{}} & \gamma _{21,3}^{{}} & \gamma _{31,3}^{{}} \\ \end{matrix} \right|_{{}}^{T}$

В качестве модели динамики можно взять:

$\mathbf{x}_{\gamma, k+1} = \mathbf{x}_{\gamma, k} + \mathbf{w}_{\gamma, k+1},$

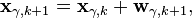
где 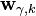$\mathbf{w}_{\gamma,k}$ - вектор-столбец нормального независимого случайного процесса.

Модель наблюдений

В качестве измерений можно использовать отфильтрованные величины скачков, которые формировать по аналогии с тем, как это делалось ранее.

Итак, модель наблюдений:

• Скачки из фазы циклограммы 1 в фазу циклограммы 2

$J_{21}^{1\to 2} = \gamma_{21,2} - \gamma_{21,1};$

$J_{31}^{1\to 2} = \gamma_{31,2} - \gamma_{31,1};$

• Скачки из фазы циклограммы 2 в фазу циклограммы 3

$J_{21}^{2\to 3} = \gamma_{21,3} - \gamma_{21,2};$

$J_{31}^{2\to 3} = \gamma_{31,3} - \gamma_{31,2};$

• Скачки из фазы циклограммы 3 в фазу циклограммы 1

$J_{21}^{3\to 1} = \gamma_{21,1} - \gamma_{21,3};$

$J_{31}^{3\to 1} = \gamma_{31,1} - \gamma_{31,3},$

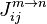где $J_{ij}^{m\to n}$ - измеренный скачок при переключении из фазы циклограммы m в фазу циклограммы n для наблюдений первой разности фаз i-ой и j-ой приемной точки.

Тогда вектор наблюдений:

$\mathbf{z}_{\gamma }^{{}}=\left| \begin{matrix} J _{21}^{1\to 2} & J _{31}^{1\to 2} & J_{21}^{2\to 3} & J_{31}^{2\to 3} & J_{21}^{3\to 1} & J_{31}^{3\to 1} \\ \end{matrix} \right|_{{}}^{T}$

Матрица измерений:

$\mathbf{H}_{\gamma }^{{}}= \left| \begin{matrix} -1 & 0 & 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \\ 1 & 0 & 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 & 0 & -1 \\ \end{matrix} \right|$

Определитель этой матрицы равен нулю, фильтр неработоспособен.

Рекурсивные уравнения фильтрации

В качестве фильтра берем Калмана с коэффициентами установившегося режима

$\mathbf{x}_{\gamma, k} = \mathbf{x}_{\gamma, k-1} + \mathbf{K}_{\gamma}\mathbf{u}_{d,\gamma,k},$

где $\mathbf{u}_{d,\gamma,k} = \mathbf{z}_{\gamma,k} - \mathbf{H_{\gamma}}\mathbf{x}_{\gamma,k-1}$.

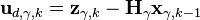Попытка 2

Параметры 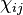$\chi_{ij}$ не зависят от спутника. По хорошему, для них нужен общий фильтр.

Рассмотрим случай двух спутников. Введем параметры:

$\chi_{1} = \chi_{25} - \chi_{14};$

$\chi_{2} = \chi_{36} - \chi_{14};$

$\chi_{3} = \chi_{24} - \chi_{16};$

$\chi_{4} = \chi_{35} - \chi_{16};$

$\chi_{5} = \chi_{26} - \chi_{15};$

$\chi_{6} = \chi_{34} - \chi_{15}.$

Вектор состояния

Тогда вектор состояния превращается в:

$\mathbf{x}_{\chi }^{{}}=\left| \begin{matrix} \chi_{1} & \chi_{2} & \chi_{3} & \chi_{4} & \chi_{5} & \chi_{6} & \Delta_{21}^{(1)} & \Delta_{31}^{(1)} & \Delta_{21}^{(2)} & \Delta_{31}^{(2)} \\ \end{matrix} \right|_{{}}^{T},$

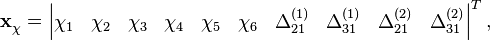
где 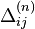$\Delta_{ij}^{(n)}$ - разность задержек i-ой и j-ой аналоговых частей для n-го спутника.

В качестве модели динамики можно опять взять:

$\mathbf{x}_{\chi, k+1} = \mathbf{x}_{\chi, k} + \mathbf{w}_{\chi, k+1},$

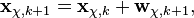
где 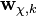$\mathbf{w}_{\chi,k}$ - вектор-столбец нормального независимого случайного процесса.

Модель наблюдений

• Для первого спутника

$J_{21,1}^{1\to 2} = \chi_{3} - \chi_{1} - \Delta_{21}^{(1)} - \Delta_{31}^{(1)};$

$J_{31,1}^{1\to 2} = \chi_{4} - \chi_{2} + \Delta_{21}^{(1)} - 2\Delta_{31}^{(1)};$

$J_{21,1}^{2\to 3} = \chi_{5} - \chi_{3} - \Delta_{21}^{(1)} + 2\Delta_{31}^{(1)};$

$J_{31,1}^{2\to 3} = \chi_{6} - \chi_{4} - 2\Delta_{21}^{(1)} + \Delta_{31}^{(1)};$

$J_{21,1}^{3\to 1} = \chi_{1} - \chi_{5} + 2\Delta_{21}^{(1)} - \Delta_{31}^{(1)};$

$J_{31,1}^{3\to 1} = \chi_{2} - \chi_{6} + \Delta_{21}^{(1)} + \Delta_{31}^{(1)}.$

• Для второго спутника

$J_{21,2}^{1\to 2} = \chi_{3} - \chi_{1} - \Delta_{21}^{(2)} - \Delta_{31}^{(2)};$

$J_{31,2}^{1\to 2} = \chi_{4} - \chi_{2} + \Delta_{21}^{(2)} - 2\Delta_{31}^{(2)};$

$J_{21,2}^{2\to 3} = \chi_{5} - \chi_{3} - \Delta_{21}^{(2)} + 2\Delta_{31}^{(2)};$

$J_{31,2}^{2\to 3} = \chi_{6} - \chi_{4} - 2\Delta_{21}^{(2)} + \Delta_{31}^{(2)};$

$J_{21,2}^{3\to 1} = \chi_{1} - \chi_{5} + 2\Delta_{21}^{(2)} - \Delta_{31}^{(2)};$

$J_{31,2}^{3\to 1} = \chi_{2} - \chi_{6} + \Delta_{21}^{(2)} + \Delta_{31}^{(2)}.$

Тогда вектор наблюдений:

$\mathbf{z}_{\gamma }^{{}}=\left| \begin{array}{cccccccccccc} J _{21,1}^{1\to 2} & J _{31,1}^{1\to 2} & J_{21,1}^{2\to 3} & J_{31,1}^{2\to 3} & J_{21,1}^{3\to 1} & J_{31,1}^{3\to 1} & J _{21,2}^{1\to 2} & J _{31,2}^{1\to 2} & J_{21,2}^{2\to 3} & J_{31,2}^{2\to 3} & J_{21,2}^{3\to 1} & J_{31,2}^{3\to 1} \\ \end{array} \right|_{{}}^{T}$

Матрица измерений:

$\mathbf{H}_{\chi}=\left| \begin{array}{rrrrrr|rr|rr} -1 & 0 & 1 & 0 & 0 & 0 & -1 & -1 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 & 1 & -2 & 0 & 0 \\ 0 & 0 & -1 & 0 & 1 & 0 & -1 & 2 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 & -2 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & -1 & 0 & 2 & -1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & -1 & 1 & 1 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & -1 & -1 \\ 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & -2 \\ 0 & 0 & -1 & 0 & 1 & 0 & 0 & 0 & -1 & 2 \\ 0 & 0 & 0 & -1 & 0 & 1 & 0 & 0 & -2 & 1 \\ 1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 2 & -1 \\ 0 & 1 & 0 & 0 & 0 & -1 & 0 & 0 & 1 & 1 \\ \end{array} \right|$

Определитель матрицы опять равен нулю...

Рекурсивные уравнения фильтрации

В качестве фильтра берем Калмана с коэффициентами установившегося режима

$\mathbf{x}_{\chi, k} = \mathbf{x}_{\chi, k-1} + \mathbf{K}_{\chi}\mathbf{u}_{d,\chi,k},$

где $\mathbf{u}_{d,\chi,k} = \mathbf{z}_{\chi,k} - \mathbf{H}_{\chi}\mathbf{x}_{\chi,k-1}$.

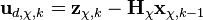Попытка 3

Попытки оценить значения задержек не увенчались успехом, что объяснимо:

• Попытки по наблюдаемым суммам определить слагаемые редко приводят к результатам;
• Слишком уж всё некрасиво и объемно получалось бы, даже если математика проходила.

Но нам оно и не надо. Нам нужно избавиться от паразитных слагаемых во вторых разностях фаз.

Модель измерений вторых разности фаз

Принимаем приближение, что коммутатор в каждом своем положении даёт одинаковый фазовый сдвиг для сигнала как первого, так и второго спутника (в зависимости от модели описания коммутатора, разница если и есть, то в сотые доли радиана). Тогда для измерений вторых разностей фаз можно записать следующую модель (см. выкладки для первых разностей фаз):

• в фазе 1 циклограммы:

$\Delta\psi_{21,izm} = \Delta\psi_{21} + \left( \Delta_{21}^{(2)} - \Delta_{21}^{(1)} \right);$

$\Delta\psi_{31,izm} = \Delta\psi_{31} + \left( \Delta_{31}^{(2)} - \Delta_{31}^{(1)} \right);$

• в фазе 2 циклограммы:

$\Delta\psi_{21,izm} = \Delta\psi_{21} - \left( \Delta_{31}^{(2)} - \Delta_{31}^{(1)} \right);$

$\Delta\psi_{31,izm} = \Delta\psi_{31} + \left( \Delta_{21}^{(2)} - \Delta_{21}^{(1)} \right) - \left( \Delta_{31}^{(2)} - \Delta_{31}^{(1)} \right);$

• в фазе 3 циклограммы:

$\Delta\psi_{21,izm} = \Delta\psi_{21} - \left( \Delta_{21}^{(2)} - \Delta_{21}^{(1)} \right) + \left( \Delta_{31}^{(2)} - \Delta_{31}^{(1)} \right);$

$\Delta\psi_{31,izm} = \Delta\psi_{31} - \left( \Delta_{21}^{(2)} - \Delta_{21}^{(1)} \right),$

где

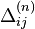$\Delta_{ij}^{(n)}$ - разность фазовых набегов в i-ой и j-ой аналоговых частей для n-го спутника,

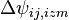$\Delta\psi_{ij,izm}$ - измеренная вторая разность фаз i-ой и j-ой приемной точки (2 спутник минус 1),

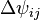$\Delta\psi_{ij}$ - истинная вторая разность фаз i-ой и j-ой приемной точки (2 спутник минус 1).

Дополнительный вектор состояния

Как видно из модели измерений разности фаз, для получения истинных вторых разностей из измеренных достаточно оценить два параметра:

$\nabla_{21} = \Delta_{21}^{(2)} - \Delta_{21}^{(1)};$

$\nabla_{31} = \Delta_{31}^{(2)} - \Delta_{31}^{(1)}.$

Соберем из них вектор состояния для будущего фильтра:

$\mathbf{x}_{\nabla } =\left| \begin{matrix} \nabla_{21} \\ \nabla_{31} \\ \end{matrix} \right|$

В качестве модели динамики можно взять:

$\mathbf{x}_{\nabla, k+1} = \mathbf{x}_{\nabla, k} + \mathbf{w}_{\nabla, k+1},$

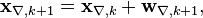
где 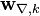$\mathbf{w}_{\nabla,k}$ - вектор-столбец нормального независимого случайного процесса.

Модель наблюдений

В качестве измерений можно использовать отфильтрованные величины скачков, которые формировать по аналогии с тем, как это делалось ранее. Сформируем из этих скачков разность вида: "скачок для первого спутника минус скачок для второго спутника".

Итак, модель наблюдений:

• Скачки из фазы циклограммы 1 в фазу циклограммы 2

$J_{\nabla, 21}^{1\to 2} = - \nabla_{21} - \nabla_{31};$

$J_{\nabla, 31}^{1\to 2} = \nabla_{21} - 2 \nabla_{31};$

• Скачки из фазы циклограммы 2 в фазу циклограммы 3

$J_{\nabla, 21}^{2\to 3} = - \nabla_{21} + 2 \nabla_{31};$

$J_{\nabla, 31}^{2\to 3} = -2 \nabla_{21} + \nabla_{31};$

• Скачки из фазы циклограммы 3 в фазу циклограммы 1

$J_{\nabla, 21}^{3\to 1} = 2 \nabla_{21} - \nabla_{31};$

$J_{\nabla, 31}^{3\to 1} = \nabla_{21} + \nabla_{31},$

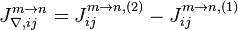где $J_{\nabla, ij}^{m\to n} = J_{ij}^{m\to n, (2)} - J_{ij}^{m\to n, (1)}$ - разность измеренных скачков при переключении из фазы циклограммы m в фазу циклограммы n для наблюдений первой разности фаз i-ой и j-ой приемной точки для двух спутников.

Тогда вектор наблюдений:

$\mathbf{z}_{\nabla}^{{}}=\left| \begin{matrix} J _{\nabla, 21}^{1\to 2} & J _{\nabla, 31}^{1\to 2} & J_{\nabla, 21}^{2\to 3} & J_{\nabla, 31}^{2\to 3} & J_{\nabla, 21}^{3\to 1} & J_{\nabla, 31}^{3\to 1} \\ \end{matrix} \right|_{{}}^{T}$

Матрица измерений:

$\mathbf{H}_{\nabla}= \left| \begin{array}{rr} -1 & -1 \\ 1 & -2 \\ -1 & 2 \\ -2 & 1 \\ 2 & -1 \\ 1 & 1 \\ \end{array} \right|$

Для этой матрицы $det \left( \mathbf{H}_{\nabla}^T \mathbf{H}_{\nabla} \right) = 108.$

Рекурсивные уравнения фильтрации

В качестве фильтра берем Калмана с коэффициентами установившегося режима

$\mathbf{x}_{\nabla, k} = \mathbf{x}_{\nabla, k-1} + \mathbf{K}_{\nabla}\mathbf{u}_{d,\nabla,k},$

где $\mathbf{u}_{d,\nabla,k} = \mathbf{z}_{\nabla,k} - \mathbf{H_{\nabla}}\mathbf{x}_{\nabla,k-1}$.

— Корогодин Илья • 10:14, 3 июня 2011 • нет комментариев

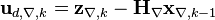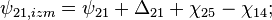
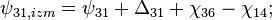
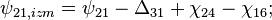
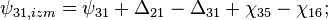
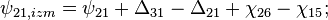
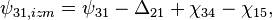
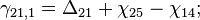
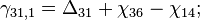
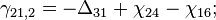
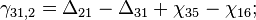
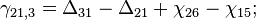
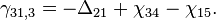
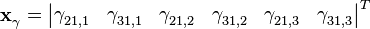
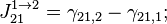
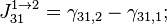
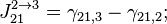
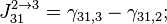
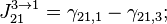
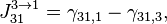
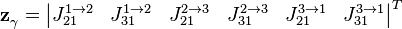
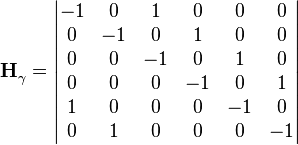
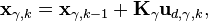
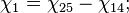
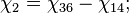
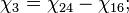
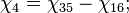
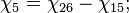
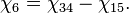
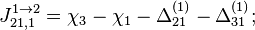
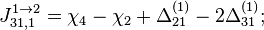
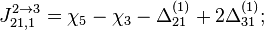
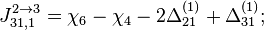
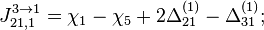
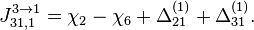
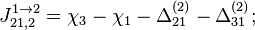
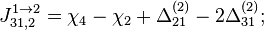
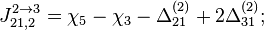
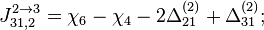
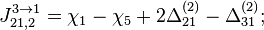
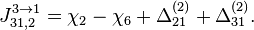
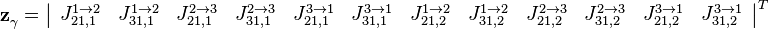
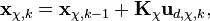
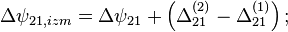
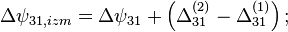
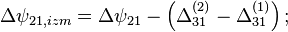
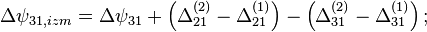
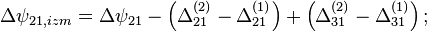
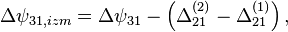
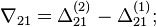
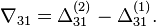
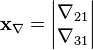
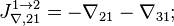
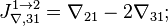
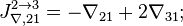
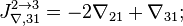
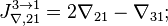
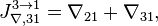
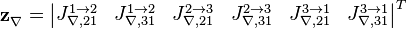
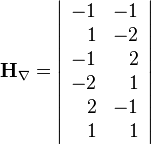
[ Хронологический вид ]Комментарии

(нет элементов)

Войдите, чтобы комментировать.